Theory

Propeller modeling using body forces

SHORTCUt achieves fast and accurate modeling of the propeller without the need to mesh the propeller geometry by using so called body forces. This means that the momentum generated by the rotating blades is directly inserted in the Navier-Stokes equation as an extra momentum source term or "body force".

Considering the momentum equation in Cartesian coordinates, the flow u=(u,v,w) is accelerated by the body force Fv=(Fvx,Fvy,Fvz). This force is only non-zero where the propeller is acting on the fluid.

$\displaystyle \frac{\partial\left(\rho u\right)}{\partial t} + \nabla \cdot \le... ...ial \tau_{yx}}{\partial y} + \frac{\partial \tau_{zx}}{\partial z} +\rho F_{vx}$ (1)
$\displaystyle \frac{\partial\left(\rho v\right)}{\partial t} + \nabla \cdot \le... ...ial \tau_{yy}}{\partial y} + \frac{\partial \tau_{zy}}{\partial z} +\rho F_{vy}$ (2)
$\displaystyle \frac{\partial\left(\rho w\right)}{\partial t} + \nabla \cdot \le... ...ial \tau_{yz}}{\partial y} + \frac{\partial \tau_{zz}}{\partial z} +\rho F_{vz}$ (3)

There are various ways to calculate the distribution of this force (Fv), how it relates to the propeller geometry and how it is affected by the propeller inflow. A range of models with various levels of complexity exist; from a simple actuator disk where the force is spread over the radius according to an ideal distribution, to a full panel code for the propeller where the force is obtained from the pressure on each panel. The strength of SHORTCUt is that the coupling and mapping between such models and the main flow solver is handled automatically. SHORTCUt also contains helpful classes that make setting up the model easier, such as:

These utilities are part of the OpenFOAM self propulsion framework that forms the core of SHORTCUt and was developed by Windén (2014). By default, SHORTCUt comes with two main propeller models (methods to calculate the body force distribution.) The Yamazaki simplified propeller model and Blade Element Momentum theory. There is also a well commented simple template model to aid users who want to implement their own model.

Yamazaki simplified propeller theory

The theory was originally developed by Yamazaki (1968) and has been further improved by Moriyama (1979) and Yamazaki (1998). It represents the action of the propeller by distributing bound vortices of strength Γ in place of the propeller blades and a free vortex with pitch h to represent the trailing wake. Γ(r,θ) is discretely distributed over a concentric grid [r,θ] centered on the propeller centroid. This achieves a hybrid theory, merging aspects of lifting line and lifting surface theory.

This distribution inherently assumes the number of blades to be infinite. While this does not allow for the flow due to individual blade passings to be studied, it gives accurate results for the average flow produced by a fast-rotating propeller. Therefore, it is suitable for coupling with RANS solvers to yield the averaged flow and forces generated by the propeller/hull interaction.

Calculating the propeller flow

Γ(r,θ) and h(r) are found iteratively from a combination of 2D airfoil theory, potential flow, the propeller inflow and the interaction of the free vortex with the blades at the propeller plane.

The velocity disturbance caused by the propeller is described by the velocity potential $\phi_{Pf\infty}$ which in turn is based on the Greens function GP. The Greens function describes the cumulative influence of Γ(r',θ') from each grid-panel on the total disturbance at [r,θ]. Here, r0 is the propeller radius and rh is the hub radius.

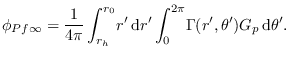$\displaystyle \phi_{Pf\infty} = \frac{1}{4\pi}\int_{r_h}^{r_0} \! r' \, \mathrm{d}r' \int_{0}^{2\pi} \! \Gamma(r',\theta')G_p \, \mathrm{d}\theta'.$ (4)
$\displaystyle G_p = \frac{r'}{h(r')R_{20}} -\frac{r\sin{(\theta'-\theta)}}{r'^2+r^2-2r'r\cos{(\theta'-\theta)}}\left(1+\frac{x}{R_{20}}\right)$ (5)

The disturbance is inversely proportional to the distance R20 from the source.

$\displaystyle R_{20} = \sqrt{x^2 + r'^2 + r^2 -2r'r\cos{(\theta'-\theta)}}$ (6)

With the disturbed velocity, the wake velocity, the propeller geometry, the strength of the bound vortices and the pitch of the free vortex known, the propeller boundary condition (velocity at the blades) can be formulated as

$\displaystyle \left(\frac{2\sqrt{r^2+a(r)^2}}{Zk_1c(r)}+\frac{r^2+h(r)^2}{2rh(r... ... + \left[u_{p\theta}(r,\theta)\right]_P\right) -\left[u_{px}(r,\theta)\right]_P$ (7)

Here, κN(r) is the Prandtl tip correction factor and k1 is an empirical correction factor for lift slope by Yamazaki (1976).

$\displaystyle \kappa_N(r) =\frac{2}{\pi}\cos^{-1}{exp\left(-Z\left(1-\frac{r}{r_0}\right)\frac{\sqrt{r_0^2+h(r)^2}}{h(r)}}\right)$ (8)
$\displaystyle {k}_1 = \left[1.07-1.05\frac{c(r)}{r_0}+0.375\left(\frac{c(r)}{r_0}\right)^2\right]_{r=0.7r_0}$ (9)

a(r) and c(r) describe the blade pitch and chord distributions, Z is the number of blades and Ω is the propeller rotation rate. The [ ]P-index indicates values on the propeller disk (x=0) and uPx(r,θ), uPθ(r,θ) are the undisturbed axial and tangential velocity distributions in the wake.

Since uPx(r,θ) and uPθ(r,θ) are defined as undisturbed, to achieve successful coupling with a RANS solver, it is necessary to know what the total induced velocities of the propeller are. These can then be deducted from RANS velocities appearing on the propeller plane to yield the undisturbed wake. The total velocities are also used to determine the momentum imparted on the fluid, from which the thrust and torque can be deduced.

$\displaystyle V_{Px} = \frac{r\Gamma(r,\theta)}{2h(r)\kappa_N(r)} +\left[\frac{... ...\overline{V}_{Px} = \frac{1}{2\pi}\int_{0}^{2\pi} \! V_{Px} \, \mathrm{d}\theta$ (10)
$\displaystyle V_{P\theta} = -\frac{\Gamma(r,\theta)}{2\kappa_N(r)} +\left[\frac... ...V}_{P\theta} = \frac{1}{2\pi}\int_{0}^{2\pi} \! V_{P\theta} \, \mathrm{d}\theta$ (11)

The pitch of the free vortex can be deduced from the directionality of the induced velocities. The pitch is averaged over the circumference (to describe a non-distorted helix) using the averaged induced velocities as

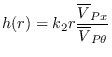$\displaystyle h(r) = k_2r\frac{\overline{V}_{Px}}{\overline{V}_{P\theta}}$ (12)

where

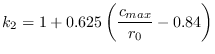$\displaystyle {k}_2 = 1+0.625\left(\frac{c_{max}}{r_0}-0.84\right)$ (13)

Equations [4] - [12] are solved iteratively until convergence of h is found.

Calculating forces

The total thrust T and the total torque Q are obtained by integrating the pressure and viscous force components resulting from the applied vortex strength and the induced momentum as

$\displaystyle T=-F_{Px} = -\rho\int_{r_h}^{r_0} \! \left(\int_{0}^{2\pi} \! \fr... ...mathrm{d}\theta +\frac{\mathrm{d}{F}_{fx}}{\mathrm{d}{r}}\right) \, \mathrm{d}r$ (14)
$\displaystyle Q=M_{Px} = \rho\int_{r_h}^{r_0} \! \left(\int_{0}^{2\pi} \! \frac... ...{d}\theta +\frac{\mathrm{d}{F}_{f\theta}}{\mathrm{d}{r}}\right) \, r\mathrm{d}r$ (15)

The pressure force components are defined as

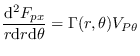$\displaystyle \frac{\mathrm{d}^2F_{px}}{r\mathrm{d}r\mathrm{d}\theta} = \Gamma(r,\theta)V_{P\theta}$ (16)
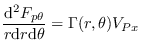$\displaystyle \frac{\mathrm{d}^2F_{p\theta}}{r\mathrm{d}r\mathrm{d}\theta} = \Gamma(r,\theta)V_{Px}$ (17)

and the viscous force components are defined as

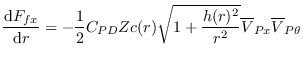$\displaystyle \frac{\mathrm{d}{F}_{fx}}{\mathrm{d}{r}} = -\frac{1}{2}C_{PD}Zc(r)\sqrt{1+\frac{h(r)^2}{r^2}}\overline{V}_{Px}\overline{V}_{P\theta}$ (18)
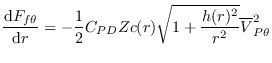$\displaystyle \frac{\mathrm{d}{F}_{f\theta}}{\mathrm{d}{r}} = -\frac{1}{2}C_{PD}Zc(r)\sqrt{1+\frac{h(r)^2}{r^2}}\overline{V}_{P\theta}^2$ (19)

Finally, the distribution of the force components over [r,θ], as defined by equations [16] - [19], are used to distribute the body force in the RANS simulation. The thrust and torque defined by equations [14] and [15] are used by the propeller controller to keep track on forces acting on the hull, based on which the RPM can be adjusted.

Apart from the propeller geometry, the user can modify the sectional drag coefficient CPD to be representative of a certain propeller. Furthermore, a correction factor acorr can be applied to the pitch a and h to account for various effects that are not covered by the theory and that might alter the flow seen by the blades at the propeller plane. For example, the "infinite blades" assumption does not capture the cascade effect.

Blade Element Momentum theory (BEMt)

Blade Element Momentum theory combines axial momentum theory and 2D blade element theory; as first suggested by Burrill (1944). The theory is suitable for calculations on marine propellers close to the design working condition. It is based on the lift and drag generated by an airfoil with the angle of attack being determined by the local pitch and the incidence of the incoming velocity which is determined by the rotation of the propeller as well as the characteristics of the nominal wake.

The coupling between blade element and momentum theory is achieved through equating their two estimates of efficiency. BEMt also requires the lift and drag properties of the blade section to be known a priori. Here, CL is estimated from the force balance of thrust in the previous iteration and CD is obtained by curve fitting to an experimentally measured CD-α curve.

The implementation of the BEMt in SHORTCUt follows the procedure by Molland et.al.(2011).

References